Post 1 Introduction to Statistical analysis of data with outliers
Post 2 Correlation when outliers in the data.
Post 3 Trend when outliers in the data.
Post 4 Correlation and trend when an outlier is added. Example.
Post 5 Compare Kendall-Theil and OLS trends. Simulations.
Post 6 Detect serial correlation when outliers. Simulations.
The posts are gathered in this pdf document.
Start of post 6: Detect serial correlation in data with outliers
This chapter deals with Monte Carlo simulations that calculate the serial correlation coefficients in noisy data. They are calculated with two different approaches. One uses the noise values, and the other uses the ranks of the noise values. Both approaches work well when the noise is white and when there is serial correlation in the noise. The approach that uses the ranks works much better than the other when there are outliers in the noise. The results are presented as probability density plots.
The mathematics to decide the serial correlation coefficients with lag 1, 2, 3 and so forth is shown in equation (3.14) in post 3 in this series. The formula uses either the noise values or the ranks of the noise values. The formula returns stable results when the noise contains many values. But it returns unstable results when the noise contains few values. Then the calculated coefficients vary, even though the noise has the same characteristics. This chapter shows how well we can calculate the serial correlation coefficients of data containing white noise, coloured noise and outliers. Due to the variability, the results are presented as probability density plots.
All simulations are done with noise data generated as described in section 5.5 in the previous post. The noise vector is first filled with white noise drawn from the standard normal distribution N(0,1). If the noise vector shall contain serial correlation, a first order Markov process with α equal to 0.20 is added to it. (A first order Markov process is also called an AR(1) process.) Thereafter, if the noise vector shall contain outliers, randomly selected 4% of the elements in the noise vector is multiplied by 20.
I tested that the formula returns correct coefficients when the data vector contained one million elements with white noise and serial correlation (α equal to 0.20). The expected lag k serial correlation coefficient is αk. Using the formula I calculated the lag 1 coefficient equal to 0.201, the lag 2 coefficient equal to 0.040 and the lag 3 coefficient equal to 0.009. These results are close to the expected values, and they show that the formula, and my implementation of it, returns correct results.
I thereafter tested noise vectors with 50 elements. This is a typical vector length when analysing climate data. In each test I did ten thousand Monte Carlo simulations, and I present the results graphically as probability density plots. The probability density is along the vertical axis and the calculated serial correlation coefficient is along the horizontal axis. Each test is done with different noise characteristics, but the ten thousand simulations in each test are done with the same noise characteristics.
6.1 Only white noise in the noise vector
Each plot presents the probability densities of the lag 1, 2 and 3 serial correlation coefficients based on 10 000 Monte Carlo simulations. Each simulation calculates the coefficients of 50 data values with white noise.The legends in Figure 6.1 to 6.9 show the means and the standard deviations of the lag 1, lag 2 and lag 3 serial correlation coefficients in the Monte Carlo simulations. The lag 1 serial coefficient is denoted by r_1, the lag 2 coefficient by r_2, and so forth.
 |
| Figure 6.2: Same as Figure 6.1, but now the serial correlation coefficients are calculated using the ranks of the noise values. |
The curves in Figure 6.1 and Figure 6.2 are almost identical. With white noise it does not matter if the coefficients are calculated with the values or with their ranks.
The probability density plots in the figures are surprisingly wide. Even when there is no serial correlation in the noise, there is a considerable probability to calculate serial correlation coefficients larger than 0.3 in absolute value. Therefore, with only one measurement series of 50 values it is not possible to calculate trustworthy serial correlation coefficients.
Serial correlation may be a problem when analysing monthly climate data. Climate is average weather during at least 30 years, and the number of months in climate analysis is therefore usually 360 or more. I therefore repeated the calculations behind Figure 6.1 with 360 noise values in each Monte Carlo simulation.
 |
| Figure 6.3: Same as Figure 6.1, but now using 360 instead of 50 data values in each simulation. |
Figure 6.3 shows that the width of the probability density plots is reduced to a third when the number of noise values is 360 compared to when it is 50. But the standard deviation is still 0.05, and the calculated serial correlation must therefore still be carefully evaluated before being applied further in the analysis.
6.2 Serial correlation in the noise vector
Each plot presents the probability densities of the lag 1, 2 and 3 serial correlation coefficients based on 10 000 Monte Carlo simulations. Each simulation calculates the coefficients of 50 data values with white noise and serial correlation. |
| Figure 6.5: Same as Figure 6.4, but now the serial correlation coefficients are calculated using the ranks of the noise values. |
The curves in Figure 6.4 and Figure 6.5 are almost identical. With white noise and serial correlation in the data it does not matter if the coefficients are calculated with the values or with their ranks.
The expected mean value of the lag 1 serial correlation is equal to 0.20 when a first order Markov process with α equal to 0.20 is added to the white noise. The mean of the calculated lag 1 serial coefficients is 0.16, which is less than the expected value. That is due to few values in each simulation.
6.3 Outliers in the noise vector
Each plot presents the probability densities of the lag 1, 2 and 3 serial correlation coefficients based on 10 000 Monte Carlo simulations. Each simulation calculates the coefficients of 50 data values with white noise and outliers.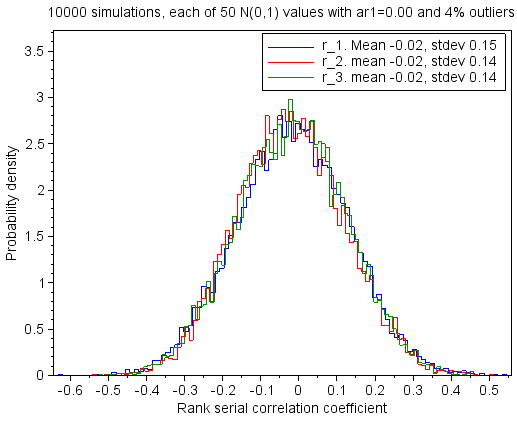 |
| Figure 6.7: Same as Figure 6.6, but now the serial correlation coefficients are calculated using the ranks of the noise values. |
When the coefficients are calculated based on the values in the noise vector (Figure 6.6), the lag 1 probability density plot differs more from that of the normal distribution than it does when there were no outliers in the noise vector, and the lag 2 and 3 probability density plots are not so wide.
When the coefficients are calculated based on the ranks of the values in the noise vector (Figure 6.7), the probability density plots are almost identical to the probability density plots that were calculated when there were no outliers in the noise.
6.4 Both serial correlation and outliers in the noise vector
Each plot presents the probability densities of the lag 1, 2 and 3 serial correlation coefficients based on 10 000 Monte Carlo simulations. Each simulation calculates the coefficients of 50 data values with white noise, serial correlation and outliers. |
| Figure 6.9: Same as Figure 6.8, but now the serial correlation coefficients are calculated using the ranks of the noise values. |
The probability density plots in Figure 6.8 and Figure 6.9 are different. The outliers cause the calculation of the lag 1 coefficient to fail when the calculation is done with the values. It fails because the serial correlation in the data is partly hidden by the outliers, and the mean of the calculated lag 1 coefficients is halved compared to what it was without the outliers. But when the calculation is done with the ranks of the values, the calculation of the coefficients is OK.
Previous post in the series




Ingen kommentarer:
Legg inn en kommentar