HSS fjerner først effekten av langtidstrender, og deretter bruker de resultatene til å vurdere langtidstrender. Dette er en metodefeil, for de kan ikke finne langtidstrender etter at effekten av dem er fjernet. Både metodikken og konklusjonene deres blir sterkt kritisert av mange kompetente klimaforskere, bl.a. av Rasmus Benestad på Real Climate og Hans Olav Hygen på Klimarealisme. I dette blogginnlegget vil jeg med et tankeeksperiment demonstrere at metodikken til HSS er fullstendig uegnet til å analysere langsiktige trender.
Humlums beregninger
HSS regner på temperaturer fra flere temperaturserier. For hver serie studerer de samvariasjonen mellom temperatur og global atmosfærisk CO2 for perioden januar 1980 til desember 2011. Jeg regner meg frem til den samme samvariasjonen som HSS gjør. Korttidsendringer i CO2 er faseforskjøvet ca 11 måneder etter korttidsendringer i temperatur. HSS bruker dette som belegg for sin påstand om at naturlige temperaturendringer har forårsaket økningen i atmosfærisk CO2 i de siste 31 årene.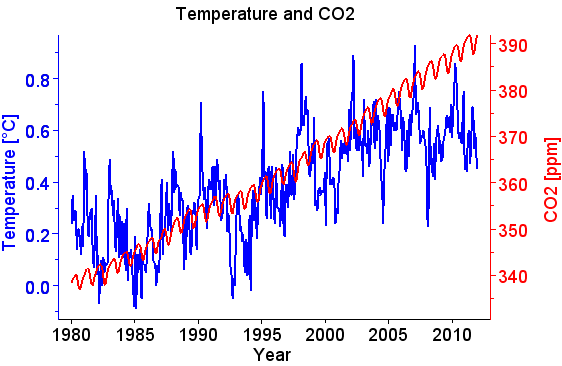 |
| Figur 1: Global temperatur (GISTEMP, blå) og global CO2 (ESRL, rød) for 1980 til 2011. |
De månedlige CO2 verdiene er fra NOAA ESRL [2]. De er beregnet fra januar 1980 på grunnlag av målinger i et globalt nettverk av stasjoner. CO2 verdiene har benevning ppm (parts per million).
GISTEMP er månedlige globale temperaturer fra NASA GISS [3]. De er avvik fra månedlig middeltemperatur, og de har benevning °C.
CO2 verdiene stiger med 1,66 ppm per år med overlagrete korttidsvariasjoner. Sesongvariasjonene er de mest iøynefallende korttidsvariasjonene. Det er mest vegetasjon på den nordlige halvkulen, og derfor er den totale fotosyntesen størst når det er sommer der og minst når det er vinter der. Sesongvariasjonen er fallende når fotosyntesen er sterk og stigende når den er svak. Det er også andre korttidsvariasjoner i CO2 konsentrasjonen.
HSS beregner 12 måneders glidende middelverdier for både CO2 og temperatur. Sesongvariasjonene i CO2 fjernes med denne midlingen, mens de andre korttidsvariasjonene og langtidstrenden beholdes. Deretter beregner HSS differansen mellom middelverdien i en måned og middelverdien 12 måneder tidligere. HSS kaller denne differansen DIFF12.
 |
| Figur 2: DIFF12 for global temperatur (GISTEMP, blå) og global CO2 (ESRL, rød). |
Figur 2 viser DIFF12 for global temperatur og for global CO2. Hver månedlige DIFF12 verdi plottes i den siste måneden som bidrar med data til verdien. Eksempelvis er DIFF12 i august 2011 gjennomsnittet av verdiene i september 2010 til august 2011 minus gjennomsnittet i september 2009 til august 2010.
DIFF12 er endring over ett år, dvs. den deriverte av den opprinnelige verdien. Middelverdien av DIFF12 for CO2 i Figur 2 er 1,67 ppm/år. Langtidstrenden til CO2 beregnet med lineær regresjonsanalyse er 1,66 ppm/år, dvs. praktisk talt den samme. Verdiene er ikke eksakt like, fordi utregningene er forskjellige.
HSS viser de samme DIFF12 kurvene i sin figur 3 i [1]. HSS angir benevningene feilaktig som henholdsvis [°C] og [ppm], mens de jo skal være [°C/år] og [ppm/år]. Det kan være denne feilen som forleder HSS til å tro at de beregner korrelasjonen mellom temperatur og CO2 vha. DIFF12 verdiene.
Figur 2 viser en klar sammenheng mellom DIFF12 for temperatur og for CO2. CO2 kurven er faseforskjøvet noen måneder etter temperaturkurven. Samvariasjon angis numerisk som en korrelasjonskoeffisient, se detaljer i appendiks A. Både HSS og jeg har beregnet korrelasjonskoeffisienten for mange forskyvninger av CO2 kurven, både frem og tilbake i tid. Forskyvningene kalles etterslep (lag på engelsk) i figurteksten og i resten av innlegget. Figur 3 viser resultatet.
 |
| Figur 3: Korrelasjonskoeffisient mellom DIFF12 for global temperatur (GISTEMP) og for global CO2 (ESRL) beregnet for mange månedlige etterslep av CO2 verdiene. |
Korrelasjonstoppen er 0,42 når DIFF12 CO2 har et etterslep på 11 måneder relativt temperaturen. Dette stemmer bra med en visuell inspeksjon av Figur 2, der CO2 kurven ligger ca 11 måneder etter temperaturkurven.
For denne kombinasjonen av temperatur og CO2 beregner HSS korrelasjonstopp 0,43 når DIFF12 CO2 har et etterslep på 9,5 måneder relativt temperaturen. De viser korrelasjonskurven grafisk i sin figur 4a i [1], og den er praktisk talt identisk med min Figur 3. Likheten viser at HSS og jeg regner likt; det er i tolkningen av resultatet jeg mener at HSS tar feil.
Vi ser på kurvene i Figur 2 når vi vurderer samvariasjonen mellom DIFF12 for temperatur og CO2. Middelverdien som kurvene varierer rundt, betyr ikke noe. Det bekreftes av formlene for korrelasjonskoeffisient i [4] og [5]. Dette oppmuntrer til å gjøre et tankeeksperiment.
Tankeeksperiment med en flat CO2 kurve
CO2 kurven i Figur 1 viser en jevnt stigende trend 1,66 ppm per år overlagret med korttidsvariasjoner. I tankeeksperimentet detrender jeg CO2 kurven slik at langtidstrenden blir null samtidig som korttidsvariasjonene beholdes. Jeg gjør ingen endringer med temperaturene. Figur 4 viser dataene i tankeeksperimentet.
 |
| Figur 4: Global temperatur (GISTEMP, blå) og detrendet global CO2 (ESRL, rød) for 1980 til 2011. |
Skalaene i Figur 1 og Figur 4 er like. Det er lettere å se korttidsvariasjonene i CO2 kurven når den er detrendet enn når den ikke er det.
Jeg gjentar HSS sine beregninger med dataene i Figur 4. DIFF12 blir som vist i Figur 5.
 |
| Figur 5: DIFF12 for global temperatur (GISTEMP, blå) og detrendet global CO2 (ESRL, rød). |
Det er identisk form på DIFF12 kurvene i Figur 5 og i den tilsvarende Figur 2 der CO2 dataene ikke er detrendet. Middelverdiene til DIFF12 for CO2 er forskjellige i de to figurene, men det betyr ikke noe når vi regner ut korrelasjonskoeffisienten.
Figur 6 viser beregnet korrelasjonskoeffisient som funksjon av etterslepet til detrendet CO2.
 |
| Figur 6: Korrelasjonskoeffisient mellom DIFF12 for global temperatur (GISTEMP) og detrendet global CO2 (ESRL) beregnet for mange månedlige etterslep av CO2 verdiene. |
Figur 6 er identisk med den tilsvarende Figur 3 der CO2 dataene ikke er detrendet. Derfor må konklusjonen i tankeeksperimentet bli, i følge logikken til HSS, at den stigende langtidstrenden til temperaturen forårsaker en stigende langtidstrend i atmosfærisk CO2 konsentrasjon. Men i tankeeksperimentet er det ingen stigende langtidstrend i CO2 !
Vi gjør et nytt tankeeksperiment der vi bikker CO2 kurven til å peke nedover, fremdeles uten å endre korttidsvariasjonene, og gjentar beregningene. Resultatet er det samme. Dvs. at metodikken til HSS tilsier at en stigende langtidstrend i temperatur forårsaker en stigende langtidstrend i CO2, også når datagrunnlaget for beregningene er CO2 med en fallende langtidstrend ! Jeg viser ingen figurer for dette siste tankeeksperimentet.
CO2 data fra Mauno Loa. Andre globale temperaturserier
Dette blogginnlegget har vist resultater basert på globale CO2 data og på GISTEMP. De globale CO2 dataene er tilgjengelige fra januar 1980. CO2 data fra Mauno Loa [2] er tilgjengelige allerede fra mars 1958. Beregninger basert på Mauno Loa dataene fra mars 1958 gir omtrent samme resultater som beregninger basert på de globale CO2 dataene fra januar 1980. Dvs. at det gjør ingen vesentlig forskjell å øke tidsserien med nesten 22 år. Det gjør heller ingen vesentlig forskjell å bruke andre globale temperaturserier enn GISTEMP.Modelsimulering
Forfatteren av bloggen Troy's Scratchpad demonstrerer med modellsimulering at metodikken til HSS er uegnet til å påvise årsak-virkning sammenhengen mellom langtidstrendene for temperatur og CO2. Med modellsimulering kjenner forfatteren fasiten. Han går gjennom beregningene til HSS og konstaterer at konklusjonene i henhold til HSS sin metodikk ikke stemmer med fasiten. Forfatterens metode har likhetstrekk med mitt tankeeksperiment.Konklusjon
Tankeeksperimentet viser hvor gal metodikken til HSS er. Beregningene deres gir samme svar uavhengig av om den lineære langtidstrenden i CO2 dataene er stigende, flat eller fallende. Artikkelen til HSS gir derfor ingen grunn til å tvile på konsensusen blant klimaforskerene, som er at den økende konsentrasjonen av drivhusgassen CO2 er menneskeskapt, og at den er hovedårsaken til den globale temperaturøkningen.Appendiks A. Korrelasjonskoeffisienter
Korrelasjonskoeffisienten kan regnes ut på flere måter. HSS oppgir ikke hvordan de regner den ut. Pearsons formel [5] er den vanligste, og det er rimelig å anta at det er den som brukes når ikke annet er oppgitt. Med Pearson er korrelasjonstoppen 0,60 når DIFF12 CO2 har et etterslep på 10 måneder relativt temperaturen, dvs. mye høyere enn toppen til HSS i [1] og som jeg har regnet ut og viser i Figur 3.De vanligste alternativene til Pearson er rangkorrelasjonskoeffisientene Spearman og Kendall. Jeg får de samme resultatene som HSS når jeg bruker Kendalls tau-b formel, og jeg bruker derfor den i beregningene som ligger bak Figur 3 og Figur 6. Kendall er ikke følsom for slengere i dataene, og den brukes ofte i statistiske hypotesetester. Det kan derfor være riktig å bruke Kendall.
Verdien på korrelasjonskoeffisienten avhenger av om vi bruker Pearson eller Kendall. Men begge gir de samme koeffisientene for de originale CO2 dataene som for de detrendete CO2 dataene. Dvs. at Figur 6 er identisk med den tilsvarende Figur 3 også når vi bruker Pearson.
Det forrige blogginnlegget forklarte Kendalls korrelasjonskoeffisient, og det sammenlignet den med Pearson og Spearman.
Referanser
1. The phase relation between atmospheric carbon dioxide and global temperatureOle Humlum, Kjell Stordahl og Jan-Erik Solheim
2. NOAA CO2 målinger, både globale og fra Mauno Loa på Hawai
Earth System Research Laboratory (ESRL) ved National Oceanic & Atmospheric Administration (NOAA)
3. NASA GISS Globale temperaturer GISTEMP
National Aeronautics and Space Administration, Goddard Institute for Space Studies
4. Kendall tau rank korrelasjonskoeffisient
Wikipedia
5. Pearsons produkt-moment korrelasjonskoeffisient.
Wikipedia
Ingen kommentarer:
Legg inn en kommentar