Det blir ofte henvist til simuleringer med epidemimodeller for å illustrere hvordan koronapandemien kan utvikle seg avhengig av tiltakene som iverksettes. Hallvard Sandberg viste bilder fra en slik modell for noen uker siden på NRK. Bildet var antagelig fra Epidemic Calculator, som jeg fant på nettet og prøvde selv. Den bruker en SEIR modell som beskriver hvordan en epidemi brer seg i en befolkning. Jeg programmerte en variant av den med Scilab på egen PC. Jeg gjorde dette primært for selv å få bedre forståelse av hvordan slike modeller fungerer.
Epidemimodeller har mange parametre som benyttes når ligningene løses. Inkubasjonstiden og liggetid på sykehus er eksempler på slike parametre. Den første delen av dette innlegget beskriver både modellen og parametrene. Parametrene navnsettes, og det opplyses om de numeriske verdiene som Epidemic Calculator bruker. I dette innlegget kjører jeg modellen med disse parameterverdiene for å kunne sammenligne modellens resultater med Epidemic Calculator's resultater. Helt til slutt i innlegget viser jeg parameterverdiene som Folkehelseinstituttet FHI sier at de bruker i sine modeller 21. april 2020. De gjenspeiler norske forhold, og de avviker mye fra parameterverdiene som Epidemic Calculator bruker.
SEIR modellen deler befolkningen inn i de fire grupper vist under. Gruppene er godt forklart i denne videoen.
- S er forkortelse for Susceptible. Personer i denne gruppen er mottakelige for smitte, dvs. at de er hverken smittet eller har blitt immune.
- E er forkortelse for Exposed. Personer i denne gruppen har fått smitten i seg, men de har ennå ikke selv blitt smittsomme. Denne perioden varer i gjennomsnitt Tinc, som i Epidemic Calculator er 5,2 dager. Det er inkubasjonstiden.
- I er forkortelse for Infected. Personer i denne gruppen kan smitte andre. Denne perioden varer i gjennomsnitt Tinf, som i Epidemic Calculator er 2,9 dager.
- R er forkortelse for Removed. Personer i denne gruppen er enten i karantene, ferdige med sykdommen og derfor immune, eller har dødd av sykdommen. Personene i R-gruppen kan ikke smittes på nytt, og de er heller ikke smittebærende mot andre.
Epidemic Calculator starter med at hele befolkningen med noen få unntak er i S-gruppen. Disse få er i I-gruppen, og de starter epidemien ved å smitte andre. De smittede starter i E, og de går over til I etter noen dager og forårsaker så at mange nye i S blir smittet og må, som dem selv, gå gjennom E, I og R gruppene.
(SIR er en enklere modell som ikke modellerer inkubasjonstiden, dvs. at den mangler E-gruppen. Under en pandemi er det viktig å inkludere inkubasjonstiden i modellen, fordi den øker tiden fra myndighetene endrer tiltak mot pandemien til de ser hvordan endringene slår ut.)
Matematisk beskrivelse av SEIR
Epidemic Calculator modellerer overgangene mellom gruppene med fire første ordens ordinære differensialligninger, se ligningene (1) til (4). De er gjengitt på nettsiden til Epidemic calculator, og de er sentrale i SEIR.Rt angir hvor mange personer en smittet person bringer smitten videre til når ingen er immune eller syke fra før. Den starter med R0, som er det basale reproduksjonstallet. Den er høy fordi det ikke er satt i verk tiltak for å hindre smitte. Når epidemien brer seg, setter myndighetene i verk preventive tiltak, og befolkningen blir mer forsiktig, og Rt reduseres. Rt er m.a.o. en funksjon av tiden, og kalles det tidsvariable basale reproduksjonstallet. I Epidemic Calculator starter Rt på 2,2, og det reduseres til 0,73 etter 100 dager. Brukeren av kalkulatoren kan velge om, når og hvor mye Rt skal reduseres.
Rt må ikke forveksles med det effektive smittetallet, noe jeg forklarer i forbindelse med ligning (1) og i denne fotnoten 1 .
Leddene i differensialligningene er de deriverte av eksponentialfunksjoner som faller med tidskonstant T. Appendiks A forklarer dette.
I ligningene (1) til (4) er S, E, I og R andeler av befolkningen, dvs. tall mellom 0 og 1.
Ligning (1) sier at S faller proporsjonalt med produktet av I og S multiplisert med en konstant. Konstanten er Rt dividert med hvor lenge en person er smittsom.
R0 er det samme som det effektive smittetallet når epidemien begynner. Når epidemien brer seg, synker S på høyre siden av ligning (1). Antallet personer som en smittet bringer smitten videre til, reduseres derfor i forhold til hva det var i starten av epidemien. Dvs. at det effektive smittetallet synker selv om Rt holdes konstant.
Det første leddet i ligning (2) viser at de som forlater S går inn i E. Det andre leddet viser at når inkubasjonstiden er over, forlater pasientene E.
De som forlater E går inn i I. Derfor er det første leddet i ligning (3) det samme som det siste leddet i ligning (2), men med motsatt fortegn. De som forlater I går inn i R. Derfor er det siste leddet i ligning (3) det samme som leddet i ligning (4), men med motsatt fortegn. Ingen forlater R, og ligning (4) har derfor bare ett ledd.
Utvidelse av modellen
Epidemic Calculator modellerer også andelen av befolkningen som blir mildt syke, som blir så syke at de legges inn på sykehus, og som dør av sykdommen. Nettsiden gjengir parametere som de bruker i denne utvidelsen, men ikke ligningene. Jeg velger å modellere de samme gruppene.De fem nye gruppene i min modell er vist under. Den gamle R gruppen er summen av de fem nye gruppene.
- M er forkortelse for Mildt syke. Personer i denne gruppen har blitt syke, men trenger ikke behandling på sykehus. De blir friske etter i gjennomsnitt Tmild dager, som i Epidemic Calculator er 11.1 dager. Noen i denne gruppen er så mildt syke at de ikke får symptomer.
- W er forkortelse for Wait. Personer i denne gruppen har blitt syke og må senere legges inn på sykehus. Tiden fra de blir syke til de legges inn på sykehus er i gjennomsnitt Twait, som i Epidemic Calculator er 5 dager.
- H er forkortelse for Hospitalized. Personer i denne gruppen ligger på sykehus. Sykehusoppholdet er i gjennomsnitt Thosp dager, som i Epidemic Calculator er 28,6 dager.
α er andelen av de smittede som legges inn på sykehus. I Epidemic Calculator er α 0,2, dvs. 20 prosent. - D er forkortelse for Dead. Epidemic Calculator bruker dødsrate 2 prosent. Jeg velger å modellere slik at de som dør først blir lagt inn på sykehus, selv om det ikke alltid er slik i virkeligheten. I Epidemic Calculator er dødsraten 2 prosent av alle som blir syke. Med min modelleringen og disse parameterverdiene må dødsraten β være fem ganger større, dvs. 10 prosent, fordi bare en femtedel av de syke blir lagt inn på sykehus.
- R er forkortelse for Recovered. Den inneholder de som har vært syke og blitt både friske og immune.
Differensialligningen for de fem nye gruppene er:
Ligningene (5) og (6) viser at de som er smittet, går fra I til enten M eller W. Andelen som går til W er α, andelen som går til M er (1-α). I praksis vet vi ikke på forhånd hvilke pasienter som skal til M og hvilke som skal til W selv om jeg modellerer det som om vi vet.
Det første leddet i (7) sier at de som forlater W går til H.
Det siste leddet i de tre første ligningene viser at M, W og H gruppene reduseres fordi pasientene går videre i sykdomsforløpet.
Det første leddet i ligning (8), og det eneste leddet i ligning (9), viser at de som kommer ut av sykehuset er enten friske og immune (til R) eller døde (til D). Det siste leddet i ligning (8) viser at alle i M blir friske og immune.
Løsning av differensialligningene
Jeg velger å løse de åtte differensialligningene (1) til (3) og (5) til (9) numerisk med Eulers metode slik den bl.a. er beskrevet i 12.3 i dette notatet fra UIO.Ligning (10) sier at vi kjenner formelen for den deriverte av x mht. tiden t. Ligning (11) viser at vi lineariserer x(t) ved t og beregner x(t+h) vha. lineær interpolasjon. h er tidsinkrementet.
Ligning (10) og (11) viser Eulers metode for en skalar x. Modellens ordinære differensialligninger er av første orden, og i følge kapitel 12.8.2 i notatet fra UIO kan vi da erstatte skalaren x med vektoren x. I vårt tilfelle inneholder x variablene S, E, I, M, W, H, D og R.
De 8 differensialligningene i modellen angir hvordan befolkningandelene i de 8 gruppene endrer seg med tiden. Løsningen starter med et kjent utgangspunkt ved et starttidspunkt. Vi velger et tidsinkrement h. Jeg bruker 1 minutt som eksempel. Etter å ha beregnet de 8 differensialligningene første gangen, kjenner vi andelene i de 8 gruppene ett minutt etter starttidspunktet. Det er utgangspunktet for den neste runden med beregning av ligningene. Etter at den er gjort, kjenner vi andelene ved tiden to minutter etter starttidspunktet. Etter 60 slike runder med beregninger kjenner vi andelene en time etter starttidspunktet. Slik fortsetter vi til vi har beregnet så langt frem i tid som vi ønsker. Med en epidemimodell kan det typisk være et år frem i tid.
Test av løsningens nøyaktighet og sammenligning med Epidemic calculator
Eulers metode som beskrevet i (11) er enkel. Jo kortere vi velger tidsinkrementet h, jo nøyaktigere blir løsningen. Jeg sjekker nøyaktigheten i modellen ved å redusere h til jeg ser at det ikke lenger vesentlig påvirker resultatet, se Figur 1 og 2. I simuleringene som figurene viser resultatene av, bruker jeg de samme parameterverdiene som Epidemic Calculator bruker, men uten å redusere Rt etter 100 dager.Som tidligere skrevet bruker jeg de samme differensialligningene for gruppene S, E og I som Epidemic calculator. Jeg tester derfor mine resultater for disse tre gruppene mot dens resultater når heller ikke den reduserer Rt etter 100 dager.
 |
| Figur 1: Test med tidsinkrement mellom 2 dager og ett minutt. Rt er 2,2 under hele kjøringen. |
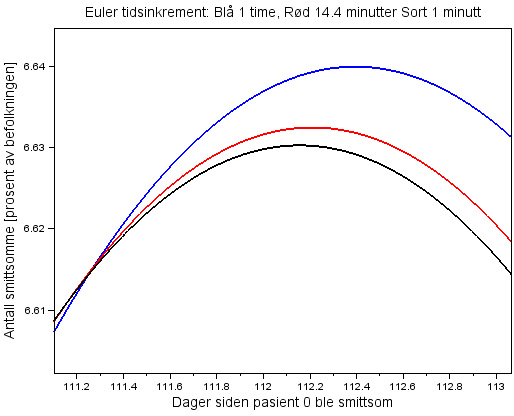 |
| Figur 2: Test med tidsinkrement 1 time, 14.4 minutter og ett minutt. Figuren er zoomet inn når antall smittete når et maksimum. Rt er 2,2 under hele kjøringen. |
I Figur 2 tester jeg med tidsinkrementene 1 time, 14.4 minutter og 1 minutt. Det midterste alternativet er fristende fordi det er 1 dag delt på 100. Med alle tre tidsinkrementene er smittetoppen på dag 112. For 1 minutt tidsinkrement er toppen 6,63 prosent av befolkningen, for 14.4 minutter 6,632 prosent og for 1 time 6,64 prosent.
Jeg kjører Epidemic Calculator med de samme parametrene. Der er smittetoppen 6,63 prosent på dag 112, dvs. det samme som jeg fikk med tidsinkrement 1 minutt. I Figur 2 ser 1 minutt riktigst ut fordi dens kurve har flyttet seg bare litt i forhold til kurven for 14,4 minutter, og fordi forflytningen er i forventet retning. Jeg velger derfor i modellen å bruke tidsinkrementet 1 minutt. Med det korte tidsinkrementet er det ikke nødvendig å programmere inn en mer komplisert løsning på differensialligningene enn Eulers metode.
Min modell gir også samme resultater som Epidemic Calculator for E, og for R før jeg utvidet modellen.
Epidemic Calculator viser ikke antall mildt syke, så der får jeg ikke sjekket den mot min modell. For andelen som må legges inn på sykehus får jeg omtrent de samme resultatene som Epidemic Calculator.
For dødsfall klarer jeg ikke å få de samme resultatene som Epidemic Calculator. Mange faktorer som ikke egner seg for matematisk beskrivelse med differensialligninger, påvirker dødsfall. Den viktigste er antagelig om sykehusene kan gi god intensivbehandling for de sykeste. Jo flere alvorlig syke, jo større er sannsynligheten for at de ikke klarer det. Jeg vet ikke hvilke vurderinger som Epidemic Calculator gjør når den beregner dødsfall.
Oppdaterte parametre fra Folkehelseinstituttet FHI.
I teksten over har jeg gjengitt parameterverdiene slik de ligger i Epidemic Calculator 20. april 2020. De er forskjellige fra verdiene som FHI opererer med. Tabellen nedenfor viser verdiene til FHI slik jeg forstår nettsiden Koronavirus-modellering ved FHI oppdatert 21. april 2020 og rapporten Situational awareness and forecasting FHI COVID-19 modelling team 20 April 2020. Parameterdefinisjonene er som tidligere i innlegget.Tinc Inkubasjonstid 3 dager
Tinf Tid smittsom 5 dager
Twait Fra syk til innleggelse 8 dager
Tmild Syk hjemme 8 dager
Thosp Liggetid på sykehus 10 dager
α Andel smittede til sykehus 1,9 prosent
Dødsrate av de smittede 0,3 prosent
β Dødsrate av de sykehusinnlagte 16 prosent
R0 Basale smittetall til 14. mars 3,11
Reff Basale smittetall fra 15. mars 0,66
FHI publiserer ikke data for hvor lenge pasienter med milde symptomer er syke hjemme hos seg selv. De belaster ikke helsevesenet, og antallet er derfor ikke interessant så lenge de respekterer karantenereglene. I modellen har jeg satt den lik gjennomsnittlig liggetid på sykehus for de som ikke trenger intensivbehandling.
FHI anslår at 40 prosent av de smittede ikke har symptomer. I min modell er de mildt syke. De bidrar til smittespredning, og de har i i følge FHI samme Tinf som de som får symptomer. Det er usikkert hvor smittefarlige de er. De hverken hoster eller nyser, og mengden virus er usikker. Men hverken de selv eller omgivelsene vet at de er smittebærere, og de kan derfor spre like mye smitte som de som får symptomer.
Liggetid på sykehus for de som ikke trenger intensivbehandling er 8 dager. Cirka 25 prosent trenger intensivbehandling. De ligger først 4 dager på vanlig sykeseng og så 12 dager på intensivavdeling, dvs. totalt 16 dager. Gjennomsnittlig liggetid på sykehus Thosp blir da (1-0,25)*8 + 0,25*16 = 10 dager.
Jeg modellerer dødsraten β blant de som er lagt inn på sykehus. FHI oppgir dødsraten blant de smittede, dvs. IFR (Infection Fatality Rate), til å være 0,3 prosent. Dødsraten i min modell er IFR dividert på α, dvs. 0,3 prosent dividert på 0,019, som er 16 prosent.
Dødsraten til FHI er veldig mye mindre enn den som Epidemic Calculator bruker. Jeg antar at det skyldes at FHI oppgir dødsrate når sykehusene har kapasitet til å intensivbehandle de som trenger det. Men også i Norge vil dødsraten øke betydelig hvis antall pasienter overstiger sykehusenes kapasitet. Jeg velger derfor å firdoble dødsraten for den andelen av pasienter som overstiger sykehuskapasiteten. Basert på tall i rapporten fra Imperial College som jeg omtalte i det forrige innlegget, antar jeg at sykehuskapasiteten for koronapasienter er 2,4 senger per 10 000 innbygger. Det er en antagelse med veldig stor usikkerhet. Men det er viktig å få frem at for å holde dødeligheten så lav som FHI oppgir, må sykehusene ha kapasitet til å gi adekvat intensivbehandling til de som trenger det.
Appendiks A. Litt om matematikken bak differensialligningene
Dette appendikset forklarer litt om bakgrunnen for differensialligningene i modellen. Det viser også noe som i teksten blir tatt tatt for gitt mht. middelverdi og tidskonstant.Det ligger en imponerende god Integral Calculator på nettet. Jeg brukte den for å finne løsningene på integralene.
Alle differensialligningene i modellen inneholder ledd som tilsvarer ligning (12), som viser hvordan antallet i en gruppe synker med tiden. Ligning (13) viser at dette leddet er den deriverte av en eksponentialfunksjon som synker med tidskonstanten T. I vår anvendelse er x(t) andelen av en gruppe som skal synke fra 1 mot 0 når tiden t går fra 0 til uendelig. Derfor må konstanten i ligning (13) være null.
Ligning (14) viser at tidskonstanten T er middelverdien av oppholdstiden i en gruppe.
Ligning (15) viser at tidskonstanten T i en synkende eksponentialfunksjon er 1,44 ganger større enn medianen (med). Jeg regner ut denne faktoren fordi noen nettsteder oppgir parameterverdier som median i stedet for som middelverdi.
Fotnoter
1I de fleste artiklene som jeg finner på nettet, er betegnelsen Rt et tidsavhengig smittetall som reduseres både pga smittehindrende tiltak og fordi flere og flere blir immune. Epidemic Calculator derimot definerer Rt slik at bare smittehindrende tiltak påvirker den. Jeg ser at en artikkel i Lancet, Early dynamics of transmission and control of COVID-19: a mathematical modelling study, definerer Rt slik Epidemic Calculator gjør. Sitat fra artikkelen: ... the time-varying basic reproduction number (Rt), defined here as the mean number of secondary cases generated by a typical infectious individual ... in a full susceptible population …' . Med denne 'støtten' fra Lancet velger jeg å bruke samme definisjon som Epidemic Calculator. Jeg kaller R0 for 'Det basale reproduksjonstallet' og Rt for 'Det tidsvariable basale reproduksjonstallet'. Oversettelsen av R0 henter jeg fra artikkelen Covid-19: Simuleringsmodeller ved epidemier.




Ingen kommentarer:
Legg inn en kommentar